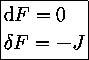As equações de Maxwell
O autor faz faz uma bellissima explanação sobre as equações de Maxwell e escreve um pouco sobre a Álgebra de Clifford e Grassmann:
As Equações de Maxwell
As chamadas equações de Maxwell (em homenagem a James Clerk Maxwell) descrevem os fenômenos eletromagnéticos (elétricos e magnéticos). Para dar uma idéia do alcance dos fenômenos regidos pelas equações de Maxwell basta lembrarmos que a luz é um fenômeno de origem eletromagnética! Desde quando formuladas, há mais de um século, estas equações passaram pelos mais severos testes experimentais e sem dúvida constituem-se num dos pilares da Física.
Estas equações foram originalmente escritas por Maxwell na forma de oito equações:
\begin{eqnarray}
\frac{\partial{B}_x}{\partial{x}}+\frac{\partial{B}_y}{\partial{y}}+\frac{\partial{B}_z}{\partial{z}}& = &0 \\
\frac{\partial{E}_z}{\partial{y}}-\frac{\partial{E}_y}{\partial{z}}& = & -\frac{\partial{B}_x}{\partial{t}} \\
\frac{\partial{E}_x}{\partial{z}}-\frac{\partial{E}_z}{\partial{x}}& = & -\frac{\partial{B}_y}{\partial{t}} \\
\frac{\partial{E}_y}{\partial{x}}-\frac{\partial{E}_x}{\partial{y}}& = & -\frac{\partial{B}_z}{\partial{t}} \\
\frac{\partial{E}_x}{\partial{x}}+\frac{\partial{E}_y}{\partial{y}}+\frac{\partial{E}_z}{\partial{z}}& = &\rho \\
\frac{\partial{B}_z}{\partial{y}}-\frac{\partial{B}_y}{\partial{z}}& = & \frac{\partial{E}_x}{\partial{t}}+J_{x} \\
\frac{\partial{B}_x}{\partial{z}}-\frac{\partial{B}_z}{\partial{x}}& = & \frac{\partial{E}_y}{\partial{t}}+J_{y} \\
\frac{\partial{B}_y}{\partial{x}}-\frac{\partial{B}_x}{\partial{y}}& = & \frac{\partial{E}_z}{\partial{t}}+J_{z}
\end{eqnarray}
Usei mathjax para mostrar as equações acima (clicando com o botão direito do mouse sobre as equações você poderá ver o código LaTeX).
Dicas de como habilitar mathjax:
https://almostrandomstuff.blogspot.com.br/2014/05/utilizando-mathjax-no-blogger.html
e
https://irrep.blogspot.com.br/2011/07/mathjax-in-blogger-ii.html
Note que:
Eq. (1) é parecida com Eq. (5);
As Eq. (2), (3) e (4) tem o campo E no lado esquerdo;
As Eq. (6), (7) e (8) tem o campo B no lado esquerdo;
Estas equações podem ser encontradas no livro "A Treatise of Electricity and Magnetism", que constitui-se em uma das grandes obras da humanidade - a primeira edição é de 1873. Na verdade Maxwell utilizou símbolos diferentes, e os usados acima correspondem ao uso moderno. Não cabe aqui explicar o significado destes símbolos; primeiro porque não é importante para o que segue, e segundo pois não deve interessar mesmo ao não-especialista. O fato é que ao escrever estas equações, Maxwell sintetizou todo o conhecimento da época acerca dos fenômenos elétricos e magnéticos na forma de um conjunto de equações relativamente simples. Apenas esse fato já mereceria destaque, mas o mais importante é que partindo destas equações Maxwell pode ir mais adiante e antecipar do ponto de vista puramente teórico descobertas experimentais que só viriam anos depois pelas mãos de Hertz.
Paralelamente (na verdade um pouco antes) ao descobrimento das equações de Maxwell desenvolvia-se na Matemática uma ferramenta chamada "cálculo vetorial". Utilizando este cálculo vetorial, as equações de Maxwell escritas acima podem ser escritas como:
\begin{eqnarray}
\nabla \cdot B & = & 0 \\
\nabla \times E & = & -\frac{\partial{B}}{\partial{t}} \\
\nabla \cdot E & = & \rho \\
\nabla \times B & = & \frac{\partial{E}}{\partial{t}}+J
\end{eqnarray}
As equações são as mesmas, mas escritas numa forma muito mais simples quando comparadas com as originais (ao invés de oito equações agora temos quatro!). As segunda, terceira e quartas equações anteriores estão agora escritas na forma da segunda equação acima, assim como a sexta, sétima e oitava estão na quarta das equações acima. Novamente cada símbolo nestas equações tem um significado que não discutiremos. A questão é: se as equações são as mesmas, o que foi feito foi trocar seis por meia-dúzia? Sim e não! Sim pois de fato as equações foram escritas de uma maneira diferente utilizando um cálculo diferente, embora bem mais simples. Mas tambem não! Não pois foi baseada na simplicidade destas equações (face às originais) que muitos desenvolvimentos foram possíveis. Nesse ponto o nome mais importante talvez tenha sido o de Heaviside. Embora não tenha sido ele o inventor propriamente dito do cálculo vetorial, foi ele quem primeiro o utilizou sistematicamente e conseguiu com isso obter avanços e descobertas que, senão impossíveis, seriam muito difíceis de obter usando as equações na forma original. A idéia equivale a dizer que como as equações são mais simples em forma então podemos compreende-las melhor e daí explorar melhor suas consequências. Se fosse apenas um trocar seis por meia-dúzia isso não seria de valor, e as pessoas continuariam escrevendo as equações de Maxwell na sua forma original.
Após o advento do cálculo vetorial, desenvolveu-se um outro tipo de cálculo em Matemática chamado "cálculo tensorial". Utilizando este cálculo tensorial, as equações de Maxwell podem ser escritas como:
\begin{eqnarray}
\partial_{\sigma} F_{\mu \nu} + \partial_{\mu} F_{\nu \sigma} + \partial_{\nu} F_{\sigma \mu} &=& 0 \label{eq:calculo_tensorial_01} \\
\partial_{\nu} F^{\mu \nu} &=& J^{\mu} \label{eq:calculo_tensorial_02}
\end{eqnarray}
Sim! Estas são as mesmas equações escritas anteriormente. Eram oito, depois quatro, e agora duas! A primeira e a segunda equações anteriores estão contidas na primeira das equações acima, enquanto a terceira e a quarta estão contidas na outra. Esquecendo o significado dos símbolos, vamos perguntar: isso é trocar seis por meia-dúzia? Novamente a resposta é sim e não! Sim pois são de fato as mesmas equações - mas num cálculo diferente. E não pois foi utilizando este cálculo tensorial que inúmeros avanços foram possíveis. Em particular, a teoria da gravitação de Einstein só foi possível de ser formulada por Einstein porque ele estudou cálculo tensorial! Com relação especifica às equações de Maxwell, o uso do cálculo tensorial permitiu compreendermos claramente a chamada covariância destas equações e o fato da eletricidade e magnetismo não serem fenômenos isolados mas sim diferentes aspectos do mesmo fenômeno eletromagnético. Esse último fato já estava claro nas equações originais de Maxwell, mas é nesta forma que a idéia torna-se mais clara pois os símbolos "E" e "B" usados naquelas equações estão agora englobados em um único símbolo "F". Novamente a simplicidade com que as equações de Maxwell podem ser escritas refletem o quão mais natural é uma ferramenta matemática dentro da atividade de pesquisa científica, no caso através do cálculo tensorial.
Embora a invenção do cálculo vetorial - o cálculo tensorial deve-se essencialmente a Ricci e Levi-Civita - esteja muitas vezes associada ao nome de Gibbs, isso é apenas meia-verdade, pois as grandes contribuições vieram mesmo de Hamilton e de Grassmann. O trabalho de Grassmann, porém, mostrou-se avançado demais para a sua época (a primeira edição de sua obra fundamental - Die Ausdehnungslehre - é de 1844), e embora tenha exercido uma certa influência sobre Gibbs (o trabalho de Gibbs é de 1881), o fez não através dos pontos mais importantes do seu trabalho. Estes pontos fundamentais só foram recuperados por Cartan quase 1 século depois de Grassmann! Fundamentando-se na estrutura algébrica desenvolvida por Grassmann, Cartan desenvolveu o cálculo de formas diferenciais, que é a base da geometria diferencial moderna. Utilizando o cálculo de formas diferenciais, as equações de Maxwell são escritas como
É sem dúvida espantosa a simplicidade destas equações, sobretudo quando comparamos com a forma inicial que estas mesmas equações foram escritas! E novamente não se trata apenas de trocar seis por meia-dúzia! O fato das equações serem mais simples reflete também o quão mais poderosa é a estrutura que estamos considerando, e nos permite obter novos resultados e ampliar nossos conhecimentos. Por exemplo, essa estrutura - a álgebra de Grassmann - é a base do conceito de super-simetria da Física Moderna, e a super-simetria é fundamental dentro de teorias como por exemplo a das super-cordas, que alguns acreditam ser a "theory of everything" - a explicação final de todos os fenômenos!.
Bem, mais simples do que estas duas equações, só mesmo uma, certo? Por isso não, eis então as equações de Maxwell:
Sim, esta equação contém a mesma informação que aquelas oito iniciais e as outras formas subsequentes. Para escrevê-las usamos uma estrutura construída sobre a da álgebra de Grassmann, a chamada álgebra de Clifford - aliás Clifford foi um dos poucos que compreendeu na época a importância do trabalho de Grassmann e por isso pode dar um passo a mais. O que essa estrutura tem a mais, além de simplificar tanto assim as equações de Maxwell? Dentre outras coisas, é nas álgebras de Clifford que aparecem objetos chamados "spinors", que são necessários para descrevermos objetos como o elétron.
Pois bem, se ao escrevermos as equações de Maxwell numa forma mais simples sempre acabamos ganhando "algo mais" ao longo da história, você pode estar se perguntando o que ganhamos com esse formalismo que nos permite escrever "as equações" como "a equação". De fato, é para suspeitarmos que haja algo por detrás de toda essa simplicidade, não? Pois é... tudo o que está por detrás disso ainda não sabemos exatamente, mas uma das ferramentas matemáticas mais poderosas desenvolvida ultimamente baseia-se nessa álgebra de Clifford e no operador de Dirac que aparece nessa equação de Maxwell. Trata-se da chamada "Geometria não-comutativa" - devida em muito a A. Connes (ganhador da Medalha Fields, maior honra quem um matemático pode receber!) - que encontra várias aplicações, por exemplo, na física de altas energias. O que mais está por detrás disso é o que devemos investigar!
Atenção: Aqui termina o texto que foi extraído Ipsis literis da página: http://www.ime.unicamp.br/~vaz/maxwell.htm
Mais informações sobre estas equações:
https://en.wikipedia.org/wiki/Electromagnetic_tensor
No link acima algumas as equações \ref{eq:calculo_tensorial_01} e \ref{eq:calculo_tensorial_02} do texto aparecem com alguns indices diferentes, mas são as mesmas equações:
$$\partial_\gamma F_{ \alpha \beta } + \partial_\alpha F_{ \beta \gamma } + \partial_\beta F_{ \gamma \alpha } = 0$$
$$\partial_\mu F^{\mu \nu} = J^\nu$$
Mais informações sobre Álgebra de Clifford:
https://revistamosaicum.org/index.php/mosaicum/article/view/231/194
Mais especificamente o trecho:
Conforme:
http://www.ifsc.usp.br/~cibelle/arquivos/tese%20Cibelle%20C%20Silva.pdf
Na página 81, Hamilton já buscava uma maneira de representar objetos geométricos através da álgebra. Outros pesquisadores tentaram, mas Grassmann prosperou mais do que os outros, aparentemente.
Clifford pode ser considerado uma figura de transição, pois escreveu depois de Grassmann e Hamilton e antes de Gibbs e Heaviside (Cibelle Celestino Silva, Tese Unicamp, 2002).
Continuarei este texto, assim que tiver tempo...